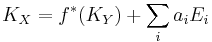Canonical singularity

In mathematics, canonical singularities appear as singularities of the canonical model of a projective variety, and terminal singularities are special cases that appear as singularities of minimal models. They were introduced by Reid (1979). Terminal singularities are important in the minimal model program because smooth minimal models do not always exist, and thus one must allow certain singularities, namely the terminal singularities.

1 Definition
2 Properties
3 Classification in small dimensions
4 Pairs
5 References

Definition

Suppose that Y is a normal variety such that its canonical class K_Y is Q-Cartier, and let f:X→Y be a resolution of the singularities of Y. Then

$\displaystyle K_X = f^*(K_Y)%2B\sum_i a_iE_i$

where the sum is over the irreducible exceptional divisors, and the a_i are rational numbers, called the discrepancies.

Then the singularities of Y are called:

terminal if a_i > 0 for all i

canonical if a_i ≥ 0 for all i

log terminal if a_i > −1 for all i

log canonical if a_i ≥ −1 for all i.

Properties

The singularities of a projective variety V are canonical if the variety is normal, some power of the canonical line bundle of the non-singular part of V extends to a line bundle on V, and V has the same plurigenera as any resolution of its singularities. V has canonical singularities if and only if it is a relative canonical model.

The singularities of a projective variety V are terminal if the variety is normal, some power of the canonical line bundle of the non-singular part of V extends to a line bundle on V, and V the pullback of any section of V^m vanishes along any codimension 1 component of the exceptional locus of a resolution of its singularities.

Classification in small dimensions

Two dimensional terminal singularities are smooth. If a variety has terminal singularities, then its singular points have codimension at least 3, and in particular in dimensions 1 and 2 all terminal singularities are smooth. In 3 dimensions they are isolated and were classified by Mori (1985).

Two dimensional canonical singularities are the same as du Val singularities, and are analytically isomorphic to quotients of C² by finite subgroups of SL₂(C).

Two dimensional log terminal singularities are analytically isomorphic to quotients of C² by finite subgroups of GL₂(C).

Two dimensional log canonical singularities have been classified by Kawamata (1988).

Pairs

More generally one can define these concepts for a pair (X,Δ) where Δ is a formal linear combination of prime divisors with rational coefficients. The pair is called

terminal if Discrep(X,Δ) >0
canonical if Discrep(X,Δ) ≥0
klt (Kawamata log terminal) if Discrep(X,Δ) >− 1 and |Δ|≤0
plt (purely log terminal) if Discrep(X,Δ) >− 1
lc (log canonical) if Discrep(X,Δ) ≥− 1.

References

Kollár, János (1989), "Minimal models of algebraic threefolds: Mori's program", Astérisque (177): 303–326, ISSN 0303-1179, MR 1040578, http://www.numdam.org/item?id=SB_1988-1989__31__303_0
Mori, Shigefumi (1985), "On 3-dimensional terminal singularities", Nagoya Mathematical Journal 98: 43–66, ISSN 0027-7630, MR 792770, http://projecteuclid.org/euclid.nmj/1118787793
Reid, Miles (1980), "Canonical 3-folds", Journées de Géometrie Algébrique d'Angers, Juillet 1979/Algebraic Geometry, Angers, 1979, Alphen aan den Rijn: Sijthoff & Noordhoff, pp. 273–310, MR 605348
Reid, Miles (1987), "Young person's guide to canonical singularities", Algebraic geometry, Bowdoin, 1985 (Brunswick, Maine, 1985), Proc. Sympos. Pure Math., 46, Providence, R.I.: American Mathematical Society, pp. 345–414, MR 927963